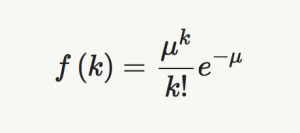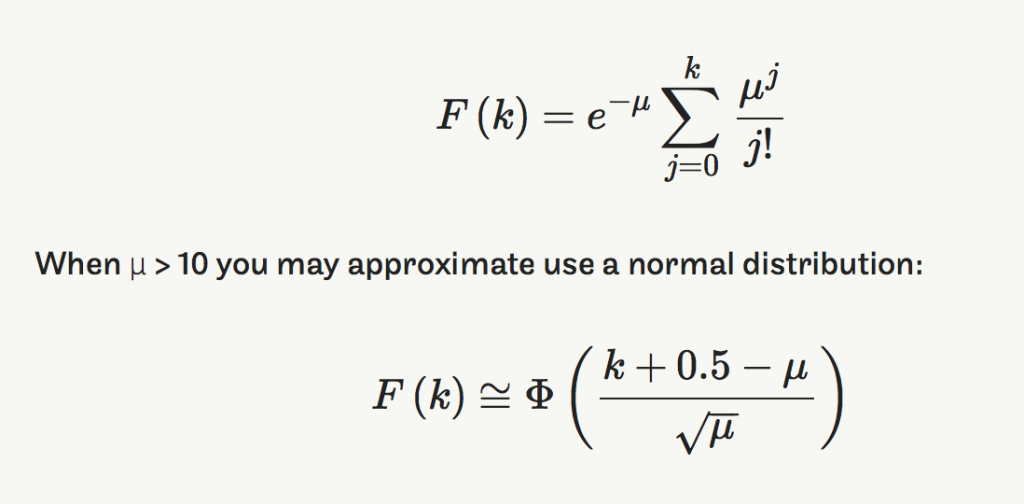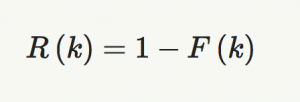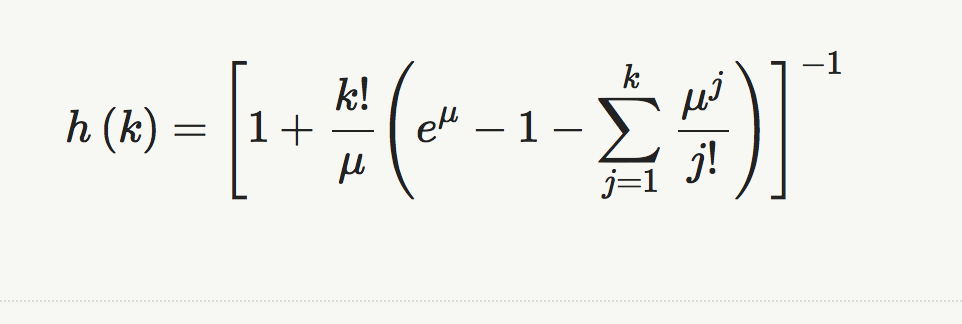This is part of a short series on the common life data distributions.
This is part of a short series on the common life data distributions.
The Poisson distribution is a discrete distribution. This short article focuses on 4 formulas of the Poisson Distribution. It is also known as the rare event distribution. It has application in a homogeneous Poisson princess and with renewal theory.
Check the following conditions to verify the process follows a Poisson distribution:
- There is a negligible or impossible chance of two simultaneous events.
- The expected value of vents in a region is proportional to the size of the region.
- The events in non-overlapping regions are independent.
If you want to know more about fitting a set of data to a distribution, well that is in another article.
It has the essential formulas that you may find useful when answering specific questions. Knowing a distribution’s set of parameters does provide, along with the right formulas, a quick means to answer a wide range of reliability related questions.
Parameters
The shape parameter, μ, is the expected number of event per time period. If modeling failure events, then μ = λt and is the average number of failures in time t.
The parameter μ is always greater than zero.
Probability Density Function (PDF)
When k ≥ 0 , k is an integer, then the probability density function formula is:
A plot of the PDF provides a histogram-like view of the time-to-failure data.
Cumulative Density Function (CDF)
F(t) is the cumulative probability of failure from time zero till time t. Very handy when estimating the proportion of units that will fail over a warranty period, for example.
Reliability Function
R(t) is the chance of survival from from time zero till time t. Instead of looking for the proportion that will fail the reliability function determine the proportion that are expected to survive.
Hazard Rate
This is the instantaneous probability of failure per unit time.
Bio:
Fred Schenkelberg is an experienced reliability engineering and management consultant with his firm FMS Reliability. His passion is working with teams to create cost-effective reliability programs that solve problems, create durable and reliable products, increase customer satisfaction, and reduce warranty costs. If you enjoyed this articles consider subscribing to the ongoing series at Accendo Reliability.