The occurrence of common cause failures (CCF) is one of the reasons why a classical reliability model of a system may dangerously underestimate the true risk of failure. CCF events directly attack the benefits of providing redundancy by creating a single point of failure. In fact, studies have shown that CCF events may contribute between 20% and 80% of the unavailability of safety systems within nuclear reactors [Werner 1994].
This post will provide an introduction into what CCFs are and why they have such a significant impact on your system.
REAL LIFE EXAMPLE
Eastern Air Lines Flight 855, flying from Miami to the Bahamas, carrying 162 passengers and 10 crew has all three engines fail due to loss of oil from missing O-ring seals. The NTSB identified the probable cause as “failure of mechanics to follow the established and proper procedures for the installation of master chip detectors in the engine lubrication system, the repeated failure of supervisory personnel … and the failure of Eastern Air Lines management…” [NTSB 1983] The failure of each engine cannot be treated as independent as they share maintenance crews, supervisors and management system.
DEFINITION
In simple terms, a CCF is the failure of multiple components from a shared event that has been transmitted through a coupling factor.
A formal definition is provided by NUREG-CR5485.
A CCF event consists of component failures that meet four criteria:
- 1. two or more individual components fail or are degraded, including failures during demand, in-service testing, or deficiencies that would have resulted in a failure if a demand signal had been received;
- 2. components fail within a selected period of time such that success of the PRA mission would be uncertain;
- 3. component failures result from a single shared cause and coupling mechanism; and
- 4. a component failure occurs within the established component boundary.
It is generally accepted that Common Cause Failures do not include those multiple component failures which fail from a functional dependency that would be modelled in a traditional fault tree or system reliability model. Instead it recognises that, in particular on redundant systems, that a dependency exists between components that were manufactured by the same company, or maintained by the same person, or exist in the same location.
EXAMPLE
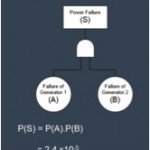
To best understand the impact for CCF, we will consider a system which consists of two backup generators in parallel. Only one generator is required to power the safety critical item, with one redundant generator in case the first fails. The generator may have a failure to start probability of P(A)=P(B)=0.0049 per demand [Vesely et al. 1994].
The probability of system failure can be calculated below to be 2.4E-5 (on demand).
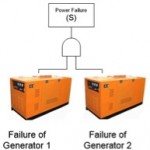
The probability of system failure can be calculated as
P(S) = P(A)P(B) = 0.0049 ´ 0.0049 = 2.4´ 10-5
Using our example, a classical Common Cause Failure may be that the two generators are maintained by the same person who was following an incorrect maintenance procedure. This means that if the first fails (due to this mistake) it is highly likely that the second will also fail. The System Reliability figure obtained above assumed that the failure of the two generators were independent. Unfortunately our coupling factor (the maintenance person and the maintenance procedure) mean that generator A and B are dependent on each other. Other examples include a manufacturing defect of a parts supplier caused defective air cleaners to be installed on both generator, or both generators existed in the same location which had a flood occur.
 MODELING CCF EVENTS
MODELING CCF EVENTS
To show the magnitude of CCF on a system, let’s briefly look at the treatment of CCF in a fault tree.
Modelling CCF events is a complex topic which cannot be covered in this article, however I will briefly show the treatment of CCF in a fault tree in order to show the magnitude of CCF on a system. To account for the CCF dependency between generator A and B, each basic failure event can be divided into a CCF element {XAB}** and an independent element {Ai},{Bi}.
**Note there are numerous methods for estimating the P(XAB) number, the NUREG-CR5485 or email me for a more comprehensive list.
 The revised probability formula is
The revised probability formula is
P(S) = P(XAB) + P(Ai) P(Bi) – P(XAB)P(Ai)P(Bi)
Then since
P(XAB) = 1.55 ´10-4 [Wierman et al. 2007, p.78]
and P(Ai) = P(Bi) = 4.745 ´10-3
the revised probability of system failure can be calculated to be 1.77 ´ 10-4. The original system failure estimate was underestimating the probability of failure by a factor of 7.4So why is CCF treated differently from any other dependency we would model in a fault tree? 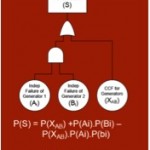 There are numerous reasons, including the following:
There are numerous reasons, including the following:
- The set of events that could be a common cause event is so huge that it would be impossible to include each as a discrete event in a reliability model, so these events get grouped into a collective group and modeled as a single type of event.
- CCF events are so infrequent that it’s unlikely for exactly the same event to occur again, so to make estimates from historic events the events are grouped into a single classification to create an empirical estimate of their effect.
It is important to recognize that CCF events are the ‘catch all’ for dependencies that are not explicitly modeled in your reliability model.
Consider the tragic Japanese Fukushima Daiichi Nuclear Power Plant failure. Despite multiple redundant methods of providing power to the plant to cool the reactors in case of an emergency, a single event caused all redundant systems to fail at once. The failure has the properties of a CCF, but in terms of reliability modeling an earthquake event was already explicitly included within the model, so the event would not be included in quantifying the nuclear reactor CCF event probability.
CONCLUSION
In equipment which requires a high level of reliability (like safety critical) redundancy is often used to meet reliability targets. Common cause failure directly attack the effectiveness of using redundancy and can seriously undermine the reliability of the system. Protection against CCF requires separation of coupling factors which provides the ability to fail due to a shared cause. Careful consideration for CCF’s must be made to ensure the probability of failure is not severely underestimated.
Bibliography
Mosleh, A., Rasmuson, D. & Marshall, F., 1998. Guidelines on Modeling Common Cause Failures in Probabilistic Risk Assessments, Washington DC: U.S. Nuclear Regulatory Commission. NUREG/CR-5485
NTSB, 1983, Aircraft Accident Report: Eastern Airlines, Inc. Lockheed L-1011, N334EA Miami International Airport, Miami, Florida, May 5, National Transportation Safety Board, Washington DC, n.d.
Vesely, W.E., Uryasev, S.P. & Samanta, P.K., 1994. Failure of emergency diesel generators: a population analysis using empirical Bayes methods. Reliability Engineering & System Safety, 46(3), 221-229.
Werner, W., 1994. Results of recent risk studies in France, Germany, Japan, Sweden and the United States, Paris: OECD Nuclear Energy Agency. NEA/CSNI/R(1994)10.
Bio:
Dr Andrew O’Connor is a reliability engineer with over 17 years of experience in asset management and the application of reliability engineering in the defense, mining, aviation, maritime and nuclear sectors. Andrew is a director of Relken Engineering (www.relken.com) and author of “Probability Distributions Used in Reliability Engineering,” Andrew’s current interested include the analysis of CMMS data to support asset decisions, the application of Bayesian networks, common cause failure modeling, uncertain evidence and probability risk assessment techniques.
 A natural question to ask when something fails is “Why did it fail”?
A natural question to ask when something fails is “Why did it fail”?

